Objective
I am currently working at Applied Research Associates (ARA) in Arlington, VA as a Mathematical Biologist. I am pleased to pursue a career in which I can apply my skills of mathematics and scientific computing.
Profile
I am a Ph.D. candidate at the University of Cincinnati studying Mathematical Biology. Over the past few years I have used experimental analyses and scientific computing to study circadian rhythms. Systems of Ordinary Differential Equations (ODEs) can be used to model the molecular components of the circadian clock. With these models, I have studied phase response to parameter perturbation, coupling between the cell division cycle and the circadian clock, and period sensitivity via bifurcation analysis.
The main focus of my dissertation is on phase response in a circadian ODE oscillator. Below, you can find an animation I have created using the matplotlib library in Python. The animation shows the time evolution of two trajectories of molecular components of the circadian clock. The trajectories have equivalent initial conditions, but the blue receives a brief pulse (parameter perturbation) at a specific phase late in the limit cycle whereas the red does not. After the blue trajectory returns to the limit cycle you can measure the resulting phase (time) delay by comparing it to the red.
Aside from simulating phase response of circadian rhythms, I have experience with additional computational, theoretical, and experimental projects. Examples of projects from my graduate career can be found below.
Projects
Below are results from projects I have worked on as a graduate student. The top row of images are all related to my work on phase response in the circadian clock. The bottom row of images showcases numerical projects I have pursued that are unrelated to my research.
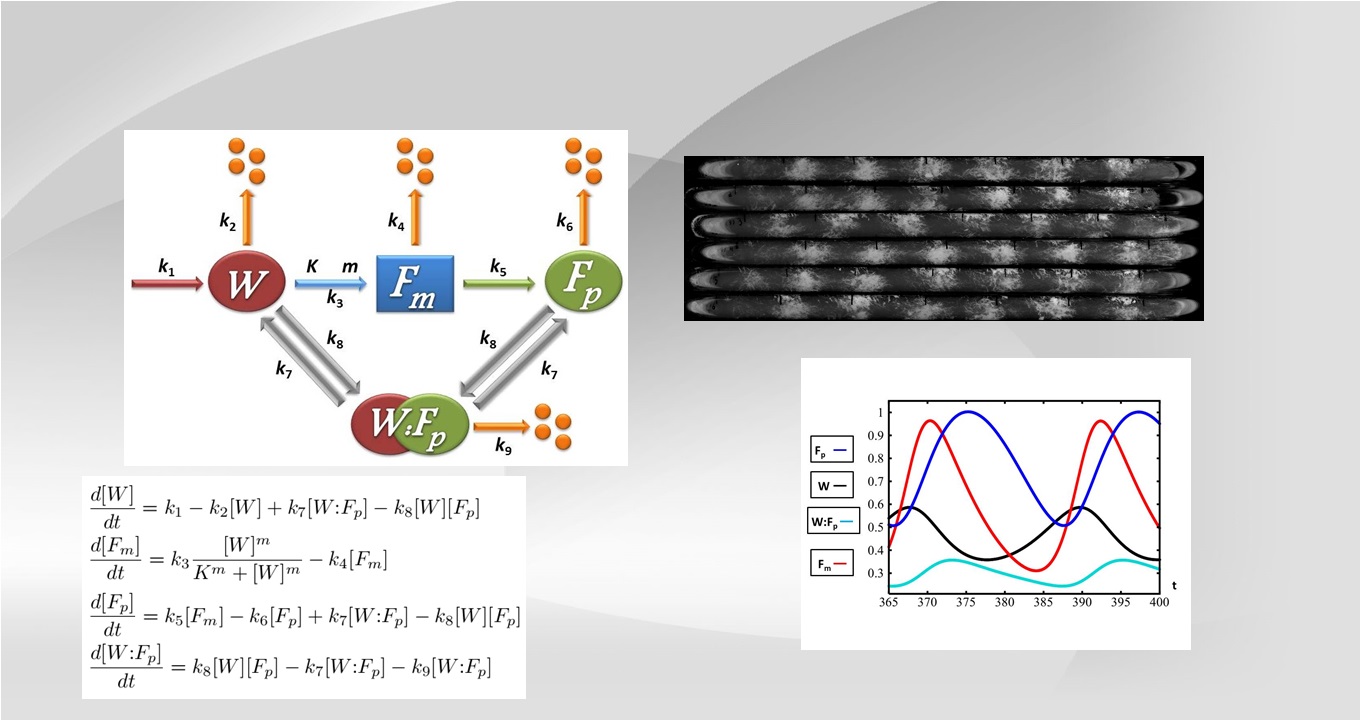
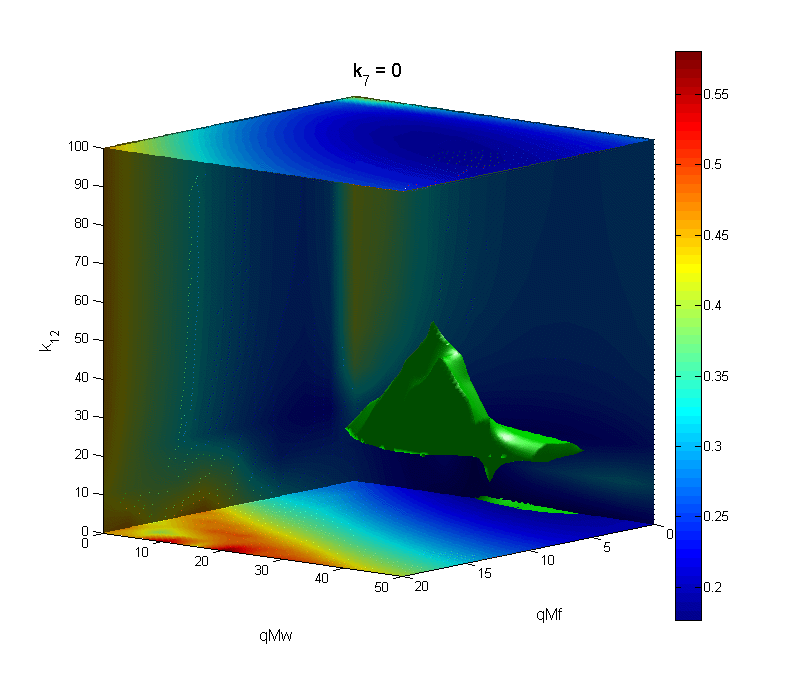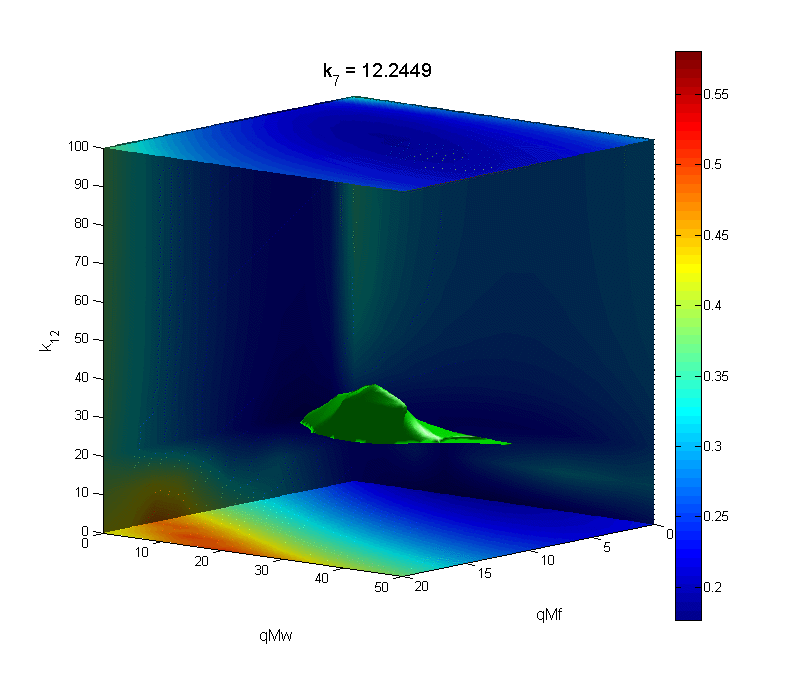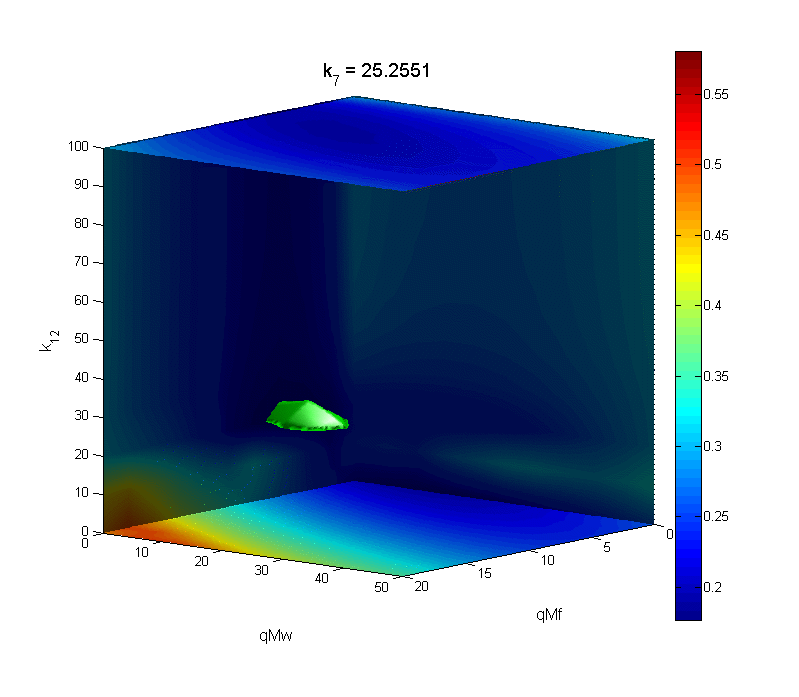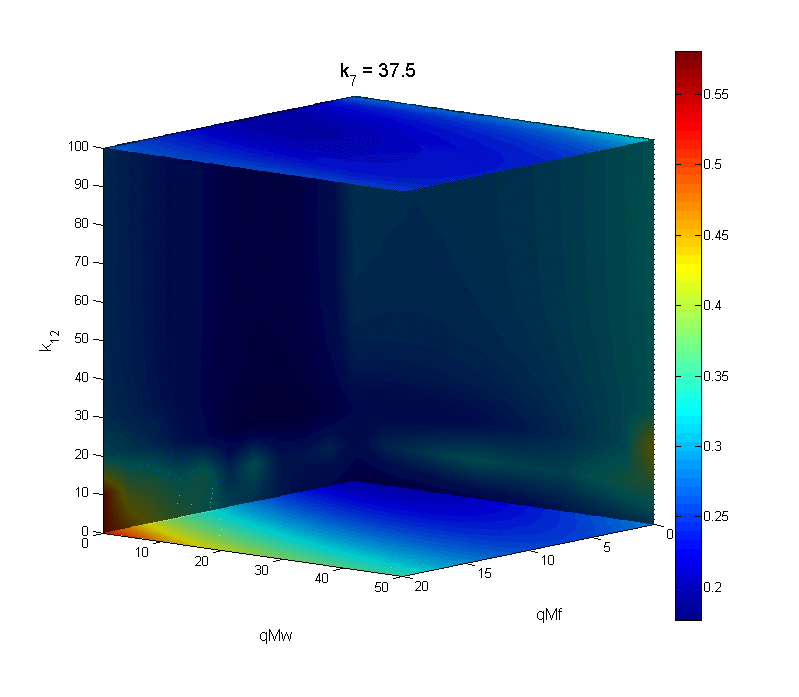
The first image sequence displays results from a circadian experiment I designed and conducted on the fungus, Neurospora, using the image processing software ImageJ. Bioluminescence shows that the top two fungus samples are out of phase with the bottom two samples. The second figure is a sample of perturbation work I have done in relation to phase response curves. Assuming a small pulse is applied to a limit cycle oscillator, it is reasonable to use perturbation theory to approximate the PRC using the infinitesimal Phase Response Curve (iPRC). The iPRC is numerically tractable, and can be extremely useful when studying the shape of the PRC. The third image sequence is an animation created with MATLAB that tracks the error of a phase response curve (against experimental data) when varying four parameters involved in the definition of the pulse. The four parameters are represented by space and time, and an isosurface (7% above the minimum error) is plotted in green for each set of parameters.
The first image in the bottom row displays an Arnold Tongue of a model which simulates a circadian clock entraining a cell division cycle (master-slave oscillator). The division cycle will have a different entrained MDT depending on the uncoupled period of the division cycle (Mass Doubling Time, or MDT) and the strength of the coupling. The region of values causing the division cycle to entrain to the circadian period is known as an Arnold Tongue. My MATLAB code for calculating the Arnold Tongue can be found here. The second image is a two-parameter bifurcation diagram of a circadian clock model. For various combinations of the two parameters shown, the limit cycle of the model can experience various period lengths (values in red). The region of oscillation is separated by a boundary of Hopf bifurcation points which cause the limit cycle to disappear when crossed. The final image sequence in the bottom row is the result of a sample fluid flow problem I have completed using the COMSOL Mutiphysics software platform. The animation shows a red ink droplet (red) being propelled down an inkjet nozzle onto paper. The original problem can be found here.

Circadian Experiments
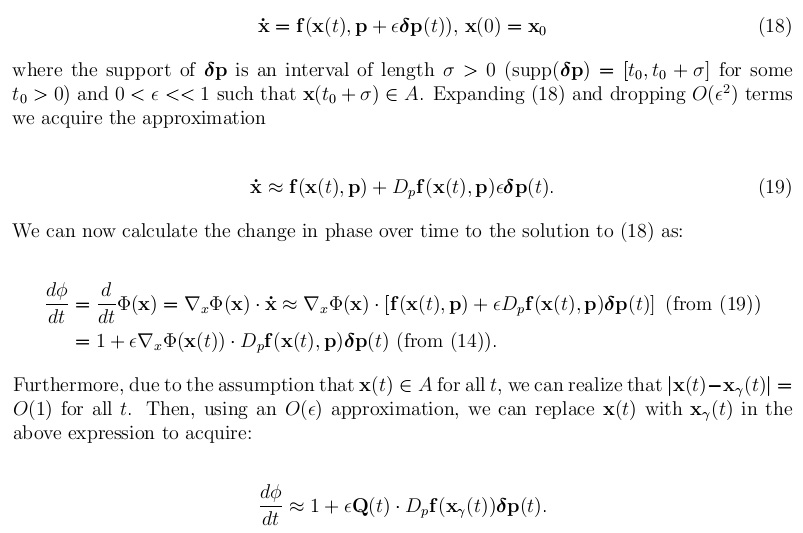
Perturbation Theory
4D Optimization
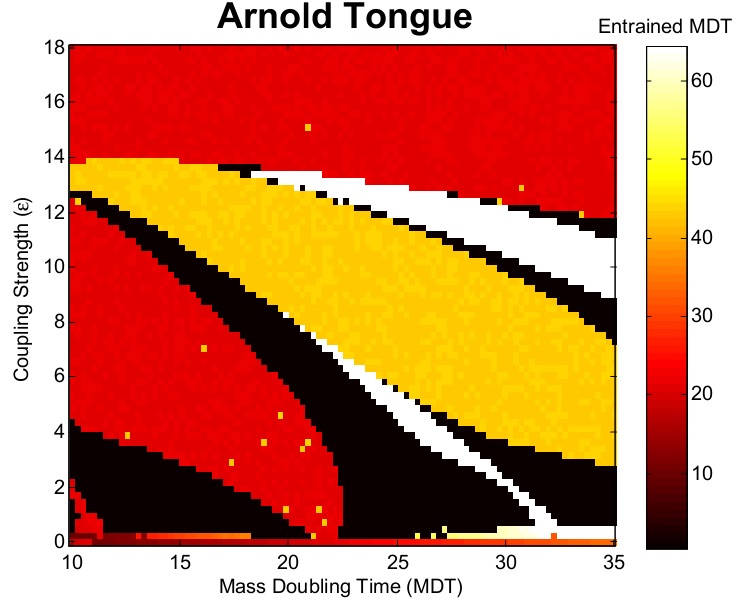
Coupled Oscillator Analysis
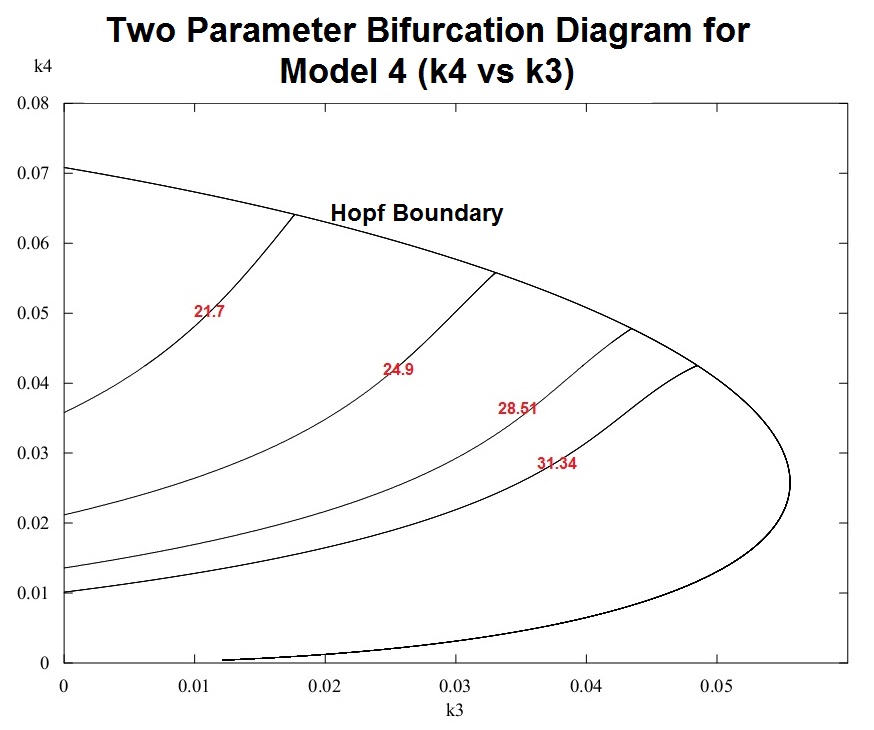
Bifurcation Theory
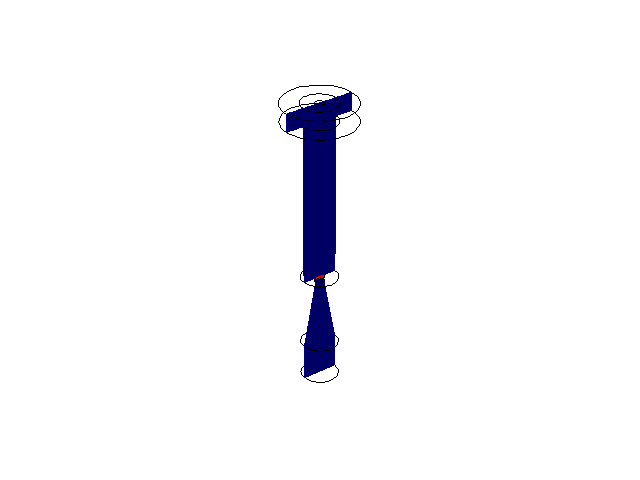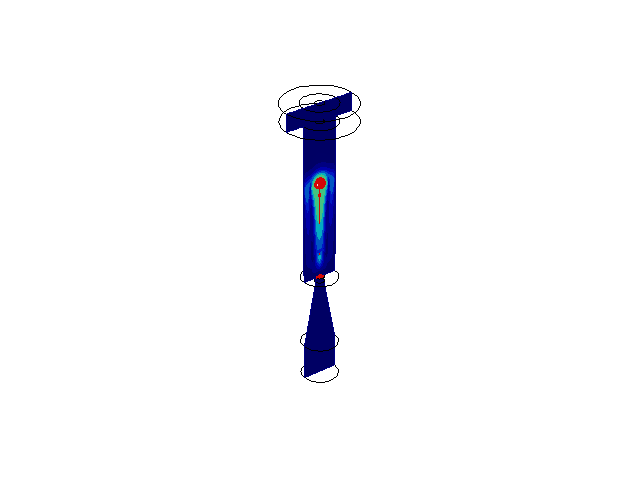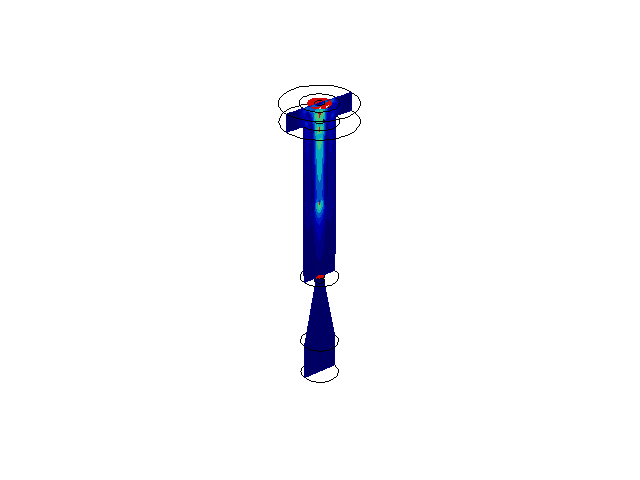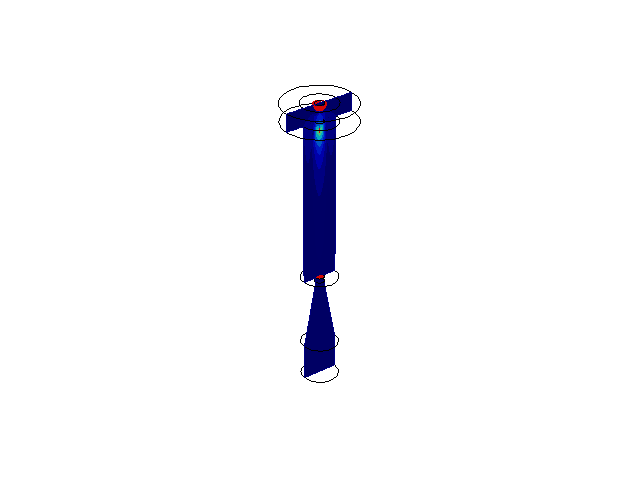
PDE Analysis